In the early days of the 2018 Major League Baseball season, I found myself in a usual April evening spot: solving math problems while watching the Red Sox dominate. On the verge of one of their 19 victories that month, Craig Kimbrel trotted out to the mound to start the top of the 9th inning.
To my dismay, play-by-play commentator Dave O’Brien was not joined in the booth by his usual, light-hearted colleague Jerry Remy. However, all was not lost because hall-of-famer Dennis Eckersley subbed in for the night. Eck, as a commentator anyway, seems to be a polarizing figure amongst Red Sox fans, especially after his spat with David Price last season. However, I always appreciate that he doesn’t hold back his opinions when he believes the manager or the players did something wrong. When he’s in the booth, there seems to be a certain level of accountability on the team’s part. Unfortunately for all baseball nerds, though, Eckersley does not take this same attitude towards the laws of physics.
Kimbrel, bent at the waist with his right arm extended, stared into the strike zone. Catcher Christian Vasquez threw down one finger without hesitation. Moments later, the text “99 mph” flashed underneath the strike zone graphic on my TV, and a major league hitter stepped out of the box, trying not to look confused by how a baseball could move in quite that way. It was in that moment that Dennis Eckersley voiced his physics gaffe: “Man that fastball’s gotta rise doesn’t it?” This isn’t the first time Mr. Eckersley has made these sorts of comments. He seems to be in search of an elusive beast, the rising fastball.
If you ask hitters, they will tell you that there’s no doubt flamethrowers like Craig Kimbrel and Aroldis Chapman can somehow heave a baseball so hard that it rises. At first glance the logic seems sound. After all, a pitcher can get a curveball to drop by applying a healthy amount of top spin. Shouldn’t it be that a pitcher could apply an equal amount of backspin and cause the ball to rise?
To answer this question, we need a slightly deeper understanding of what forces are actually acting on the baseball during its half-second voyage to the catcher’s mitt. For now, we are only considering the forces while the ball is in the air, after the pitcher releases it. In total, there are three:
-
Gravity
There will always be a gravitational force towards the earth on pitched baseballs, no matter how fast or what direction they travel. This gives baseballs their natural arc trajectory both from the mound and off the bat.
-
Drag
Since baseballs move through a fluid, in this case the same air we breathe, there is always a drag force created by the ball pushing the air out of the way. This force will always oppose the ball’s motion, slowing it down.
-
The Magnus Effect
This is the most intriguing, and strange, force encountered when examining the rising fastball. The Magnus effect (or Magnus force) is created by the baseball’s spin. Essentially, some of the air surrounding the ball “grips” the cover of the baseball and spins with it. In the case of backspin, this means the air underneath the ball moves slower than the air on top, creating higher pressure on the bottom of the ball. This pressure differential pushes the ball upward, resulting in the Magnus force.
The Magnus effect is tricky, and you can read a little more in depth about it here. For our purposes, though, it’s not all that necessary to understand the exact physical mechanisms that make a spinning ball move. The key is this: a baseball with backspin (i.e. a fastball) will have a Magnus force that points upwards.

At this point, it seems like we are closer to proving that fastballs do, in fact, rise. An upward Magnus force on fastballs is pretty damning evidence. However, we cannot forget about our other two forces. In particular, we need to remember gravity. One of the key principles of Newtonian physics is that objects accelerate in the direction of the net force on that object, or the sum of all the forces’ magnitudes and directions. This means that forces in opposite directions, but equal in magnitude, will exactly cancel each other out, but forces in the same direction will add together to make a stronger net force.
The reason baseballs always slightly drop on the way to home plate is that the gravitational force is stronger than the Magnus force. Gravity wins the tug of war match over the lift caused by backspin. The net force is still downward, albeit slightly smaller since the Magnus force pulls it up a little. In the case of a curveball, the Magnus force and gravity act together to cause the ball to drop more than normal, due to a large net force down.
This means that, if we wanted to make a fastball rise, we would need to throw it in such a way that the Magnus force is larger than gravity, creating a net force upwards. How would one do that? Well it turns out the answer comes from….math! Buckle up everybody.
The Math
Typically, physicists write the formula to calculate the magnitude of the Magnus effect as such:
Where,
the magnitude of the Magnus Force
the lift coefficient of the baseball
the density of the air
the cross sectional area of the baseball
the velocity of the baseball
The trickiest value to find here is the lift coefficient, . Essentially, it is dependent on the spin rate and speed of the baseball. However, exactly how the lift coefficient is effected by these features relies on some fairly complicated physics. Leading baseball physicist Alan Nathan has a paper dedicated to this topic here.
For the following calculations, I’m going to use David Kagan’s lift coefficient formula:
where is the velocity of the baseball in mph, and
is the spin rate of the baseball in rpm.
Now that we have an expression for the Magnus force, we can set it equal to our gravitational force and find the point at which those two forces cancel each other out. Any greater Magnus force would result in a net force upwards, and thus, a rising fastball (note: this simple model disregards the drag force, which would eventually slow the ball down enough for gravity to cause it to drop). After doing some slick algebra and simplifying the expression, we reach this formula:
The important thing to notice is that this is still an expression of two variables: spin rate and velocity. This means that as the pitcher throws the ball harder, he wouldn’t need to put as much spin on it in order to get a large Magnus force. The same is true in reverse. If a pitcher threw a baseball with incredible spin, he wouldn’t need to throw it as fast in order to achieve a rising effect.
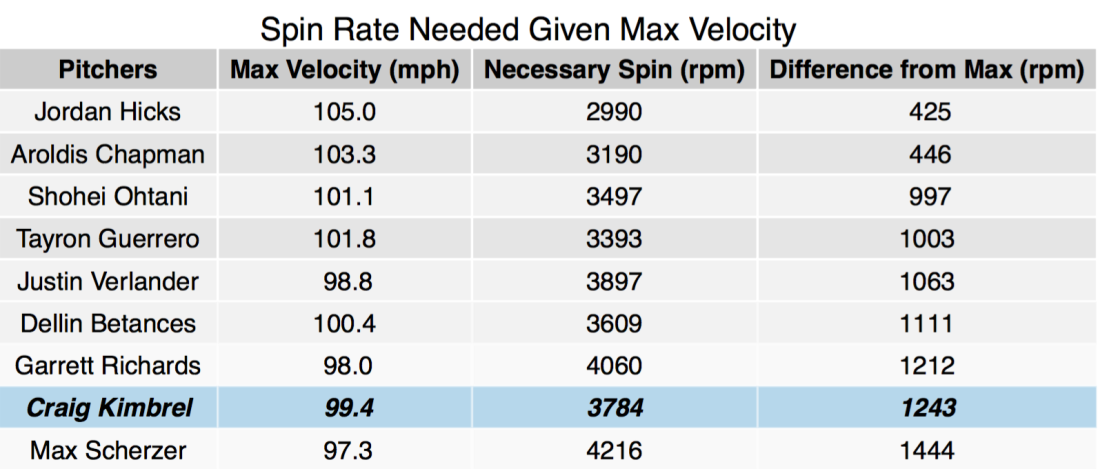
This formula is the final piece of our hunt for the rising fastball. Let’s return to our friend Craig Kimbrel. According to Statcast data, so far in 2018 Kimbrel has had an average fastball velocity of 96.6 mph, and an average spin rate of about 2380 rpm. His hardest fastball was clocked at 99.4 mph, and his largest spin rate was 2541 rpm (not on the same pitch). So how close is he to throwing a rising fastball?
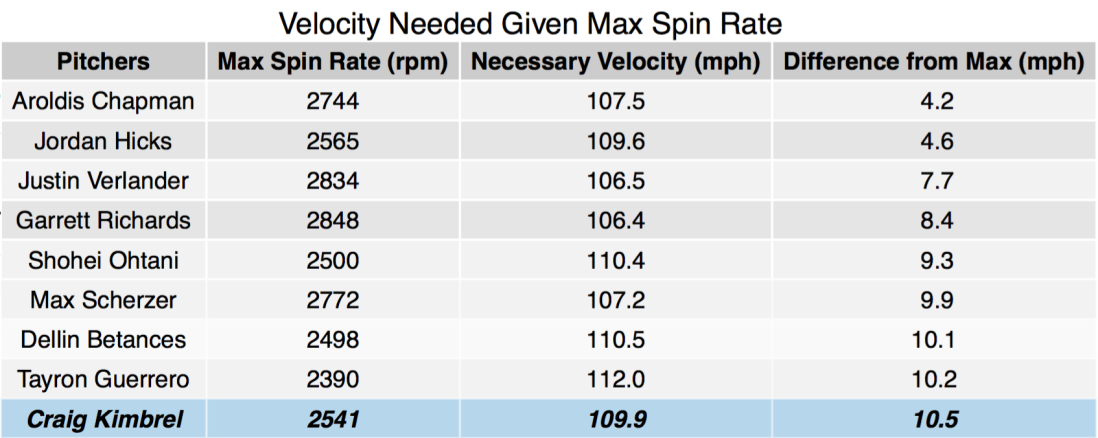
If we plug in his maximum fastball velocity to our last formula, we can calculate that he would need a spin rate over 3784 rpm in order to cause the ball to rise even slightly. Alternatively, we can take his maximum spin rate and solve for the necessary rising velocity: about 110 mph. These results are summarized in the charts below, along with a few other notable major leaguers.
This first chart shows the pitcher’s maximum fastball velocity this year, the minimum spin that they would need to put on that pitch in order for the ball to rise, and the difference between that theoretical spin rate and their maximum spin rate thrown this year:
The next chart shows the pitcher’s maximum spin rate thrown this year, the velocity that they would need on that pitch in order for the ball to rise, and the difference between that theoretical velocity and their maximum velocity thrown in 2018 so far:
But What Does it All Mean?
These charts are organized by who has the smallest difference between the theoretical limits they need to reach and their actual maximums. In other words, the pitchers are in order of who is “closest” to throwing a rising fastball. Ironically, Kimbrel is at or near the bottom of both of these charts. It also appears that Chapman is surprisingly close to getting his fastball to rise. He would only need to gain a few miles per hour on his fastest fastball!
So why do hitters swear that some talented pitchers get their fastballs to rise? It’s actually a result of their own brains tricking them. When hitters get accustomed to certain fastball velocities (say between 90 and 94 mph), their brain gets better and better at noticing the downward trajectory of the baseball. It then starts to predict with more accuracy where the pitch will end up. When the flamethrowers step on the mound and hit close to 100 mph, the ball still drops, but slightly less than slower pitches. The hitter’s brain, though, still predicts that the ball will cross the plate at a lower position than it actually does. When the ball ends up crossing the plate higher than expected, the brain reconciles this difference by making a visual adjustment, allowing the hitter “see” the ball rise up.
The charts above give a rough idea of what it would take to throw a rising fastball. However, there are a few important things to note about this data:
- All of these velocities are measured out of the hand. The drag force would actually slow the ball down considerably on it’s way to home plate, so the pitchers would likely need to throw it even harder than what’s stated here in order to get it to rise.
- The fact that the baseball is thrown from a mound allows the pitcher to throw at a downward angle to the batter. This initial downward trajectory plays into gravity’s hands, meaning the Magnus force, again, would need to be bigger than what’s stated here to throw a rising fastball.
- These charts show the maximum velocities and spin rates, which hardly ever occur on the same pitch. So when we see that Chapman is “close” to throwing a rising fastball, that is in relation to the absolute fringes of his performance.
- All calculations of the Magnus force and lift coefficient were assuming the ball was pitched at sea level. At higher elevations, the Magnus force is weaker since there’s less air to “grip” the baseball as it spins.
In most of these cases, the pitcher would need to gain over 1000 rpm on their fastest pitches, or 7 – 10 mph on their best spun fastballs. Changes of these magnitudes are virtually never seen at the major league level. It’s quite notable if a pitcher gains 2 – 3 mph on their fastball, let alone 7 – 10 mph.
However, there is a deeper problem here. Major League Baseball is currently witnessing the most impressive fastballs in history, but many scientists and doctors believe that we are reaching the limit of human capabilities in baseball velocity. A 2010 article from Popular Mechanics states that a baseball thrown at 100 mph “subjects the arm to the same amount of stress as if the pitcher had a 60-pound weight hanging from his hand in [the throwing] position.” Every time Chapman and Company flash triple digits on the ballpark radar gun, the fans clap and cheer, but the pitchers’ ulnar collateral ligaments scream. Let’s say Kimbrel did gain that 10.5 mph he needed to throw a rising fastball. It’s likely that after that he would never be able to throw another pitch, at least not without a bionic elbow.
After all of the math and physics calculations, we have come to an interesting result. The physics was never the enemy to discovering the rising fastball. Rather, it is the human body’s own fragility that limits that pesky Magnus force. The fact remains that, without some sort of artificial arm, we will never see a rising fastball thrown in a Major League Baseball game. So, the next time you’re listening to Mr. Eckersley announce a game, and he asks “That fastball’s gotta rise doesn’t it?” you can answer assuredly, “No, Eck. No it does not.”

Great article Joe! How might release point have anything to do with the “rise” of the ball? Look at Kimbrels release point which appears to be at the hitters waist level yet the pitch is caught at shoulder height? Do you still consider this a function of the hitters brain or is the ball actually rising based on the release point? Good shit though man.
LikeLike
Thanks for the read! Glad you liked it. Release point and the angle at which the ball is thrown toward the hitter certainly change things. However, in the video of Kimbrel I believe the “rising” action is actually an optical illusion resulting from the camera angle. I think his release point is higher than it seems in the video.
That said, if the ball had less of a downward trajectory from the start, then the ball would have less downward velocity. Therefore, the acceleration of the ball due to the Magnus force would make it seem like it rises more since there is less downward velocity that it has to overcome. This happens in softball all the time. Since softball pitchers throw with a more upward trajectory, the Magnus force can cause a much bigger rising appearance to the batter, since the pitch stays almost completely flat. It’s still just the hitter’s brain tricking them, but in a more noticeable way.
LikeLike